Relations and Functions Class 12 MCQ-31 to 55
Question 31.
If a relation R on the set {1, 2, 3} be defined by R = {(1, 2)}, then R is
(a) reflexive
(b) transitive
(c) symmetric
(d) None of these
Answer
Answer: (b) transitive
Question 32.
Let us define a relation R in R as aRb if a ≥ b. Then R is
(a) an equivalence relation
(b) reflexive, transitive but not symmetric
(c) neither transitive nor reflexive but symmetric
(d) symmetric, transitive but not reflexive
Answer
Answer: (b) reflexive, transitive but not symmetric
Question 33.
Let A = {1, 2, 3} and consider the relation R = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 3), (1, 3)}. Then R is
(a) reflexive but not symmetric
(b) reflexive-but not transitive.
(c) symmetric and transitive
(d) neither symmetric, nor transitive
Answer
Answer: (a) reflexive but not symmetric
Question 34.
The identity element for the binary operation * defined on Q ~ {0} as
a * b = \(\frac{ab}{2}\) ∀ a, b ∈ Q ~ {0} is
(a) 1
(b) 0
(c) 2
(d) None of these
Answer
Answer: (c) 2
Question 35.
If the set A contains 5 elements and the set B contains 6 elements, then the number of one-one and onto mappings from A to B is
(a) 720
(b) 120
(c) 0
(d) None of these
Answer
Answer: (c) 0
Question 36.
Let A = {1, 2,3,…. n} and B = { a, b}. Then the number of surjections from A into B is
(a) nP2
(b) 2n – 2
(c) 2n – 1
(d) None of these
Answer
Answer: (b) 2n – 2
Question 37.
Let f : R → R be defined by f (x) = \(\frac{1}{x}\) ∀ x ∈ R. Then f is
(a) one-one
(b) onto
(c) bijective
(d) f is not defined
Answer
Answer: (d) f is not defined
Question 38.
Let f: R → R. be defined by f (x) = 3x² – 5 and g : R → R by g (x) = \(\frac{x}{x^2+1}\). Then g o f is
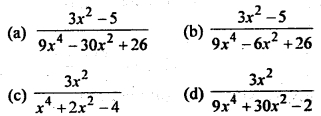
Answer
Answer: (a)
Question 39.
Which of the following functions from Z into Z are bijective?
(a) f(x) = x³
(b) f(x) = x + 2
(c) f(x) = 2x + 1
(d) f{x) = x² + 1
Answer
Answer: (b) f(x) = x + 2
Question 40.
Let f: R → R be the function defined by f(x) = x³ + 5. Then f-1 (x) is
(a) (x + 5)1/3
(b) (x -5)1/3
(c) (5 – x)1/3
(d) 5 – x
Answer
Answer: (b) (x -5)1/3
Question 41.
Let f: A → B and g : B → C be the bijective functions. Then (g o f)-1 is,
(a) f-1 o g-1
(b) f o g
(c ) g-1 o f-1
(d) g o f
Answer
Answer: (a) f-1 o g-1
Question 42.
Let f: R – {\(\frac{3}{5}\)} → R be defined by f(x) = \(\frac{3x+2}{5x-3}\) then
(a) f-1(x) = f(x)
(b) f-1(x) = -f(x)
(c ) (f o f)x = -x
(d ) f-1(x) = \(\frac{1}{19}\) f(x)
Answer
Answer: (a) f-1(x) = f(x)
Question 43.
Let f: [0, 1| → [0, 1| be defined by
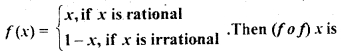
(a) Constant
(b) 1 + x
(c) x
(d) None of these
Answer
Answer: (c) x
Question 44.
Let f: |2, ∞) → R be the function defined by f(x) – x² – 4x + 5, then the range of f is
(a) R
(b) [1, ∞)
(c) [4, ∞)
(d) [5, ∞)
Answer
Answer: (b) [1, ∞)
Question 45.
Let f: N → R be the function defined by f(x) = \(\frac{2x-1}{2}\) and g: Q → R be another function defined by g (x) = x + 2. Then (g 0 f) \(\frac{3}{2}\) is
(a) 1
(b) 0
(c) \(\frac{7}{2}\)
(d) None of these
Answer
Answer: (d) None of these
Question 46.
Let f: R → R be defined by
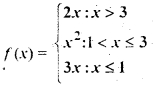
then f(- 1) + f (2) + f (4) is
(a) 9
(b) 14
(c) 5
(d) None of these
Answer
Answer: (a) 9
Question 47.
Let f : R → R be given by f (,v) = tan x. Then f-1(1) is
(a) \(\frac{π}{4}\)
(b) {nπ + \(\frac{π}{4}\) : n ∈ Z}
(c) does not exist
(d) None of these
Answer
Answer: (b) {nπ + \(\frac{π}{4}\) : n ∈ Z}
Question 48.
The relation R is defined on the set of natural numbers as {(a, b): a = 2b}. Then, R-1 is given by
(a) {(2, 1), (4, 2), (6, 3),….}
(b) {(1, 2), (2, 4), (3, 6),….}
(c) R-1 is not defined
(d) None of these
Answer
Answer: (b) {(1, 2), (2, 4), (3, 6),….}
Question 49.
The relation R = {(1,1), (2, 2), (3, 3), (1, 2), (2, 3), (1, 3)} on set A = {1, 2, 3} is
(a) Reflexive but not symmetric
(b) Reflexive but not transitive
(c) Symmetric and transitive
(d) Neither symmetric nor transitive
Answer
Answer: (a) Reflexive but not symmetric
Question 50.
Let P = {(x, y) | x² + y² = 1, x, y ∈ R]. Then, P is
(a) Reflexive
(b) Symmetric
(c) Transitive
(d) Anti-symmetric
Answer
Answer: (b) Symmetric
Question 51.
Let R be an equivalence relation on a finite set A having n elements. Then, the number of ordered pairs in R is
(a) Less than n
(b) Greater than or equal to n
(c) Less than or equal to n
(d) None of these
Answer
Answer: (b) Greater than or equal to n
Question 52.
For real numbers x and y, we write xRy ⇔ x – y + √2 is an irrational number. Then, the relational R is
(a) Reflexive
(b) Symmetric
(c) Transitive
(d) None of these
Answer
Answer: (a) Reflexive
Question 53.
Let R be a relation on the set N be defined by {(x, y) | x, y ∈ N, 2x + y = 41}. Then R is
(a) Reflexive
(b) Symmetric
(c) Transitive
(d) None of these
Answer
Answer: (d) None of these
Question 54.
Which one of the following relations on R is an equivalence relation?
(a) aR1b ⇔ |a| = |b|
(b) aR2b ⇔ a ≥ b
(c) aR3b ⇔ a divides b
(d) aR4b ⇔ a < b
Answer
Answer: (a) aR1b ⇔ |a| = |b|
Question 55.
Let R be a relation on the set N of natural numbers denoted by nRm ⇔ n is a factor of m (i.e. n | m). Then, R is
(a) Reflexive and symmetric
(b) Transitive and symmetric
(c) Equivalence
(d) Reflexive, transitive but not symmetric
Answer
Answer: (d) Reflexive, transitive but not symmetric












No comments